Games on networks, with application to Thai politics
Political conflicts are rarely between two parties. In Iraq, for example, there were as many as 19 different groups engaged, including the Islamic Army in Iraq, Al-Qaeda in Iraq, the Jihadist Leagues, and the Just Punishment Brigades. In Syria, we see a similar picture, including the Free Syrian Army, the Syrian Liberation Front, the Syrian Islamic Front, and Jabhat al-Nusra. Many attempts to understand these kinds of situations group all the rebel forces together against a government. But neither are the rebels unified, and monolithic. Nor, necessarily, is the government. We explore a theory of the interactions among these various kinds of factions in order to better understand what kinds of actions are most likely to be undertaken. To do so, we combine elements of strategic calculation and the analysis of networks. The basic insight is the old saw, often attributed to the 6th century (BCE) Chinese general, Sun Tzu: hold your friends close, and your enemies closer.
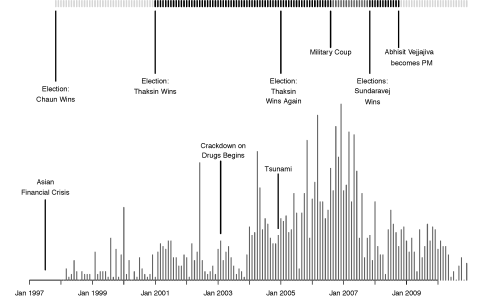
The top rug shows the different parties that are in power in Thailand during the observation period, with markers for changes in power. The bottom plot shows conflictual events in Thailand from 1998 on.
One understanding of multilateral conflicts is that if there are lots of different groups, they can gain by uniting. The network model is more nuanced and assumes that if there are two groups that are close to each other in terms of their goals and ideologies, each is likely to assume the other can take the initiative. This collective action dilemma is often described as “free riding,” wherein my group will be willing to let your group pay the costs of conflict, especially if we can share in the benefits of winning without having to be directly engaged. Groups are more likely to be engaged when they are isolated from other groups, not when they are closely aligned with them.
Our research examines this idea in the case of Thailand (2001-2010), wherein there are two major ongoing conflicts, and in which the alliances involve multiple groups in changing configurations. We collect textual descriptions of the ebb and flow of interactions among the various (four dozen) government and anti-government groups in Thailand. These are then analyzed to see whether the periods with networks which have the greatest potential for free-riding, were in fact those periods in which there was less conflict. Our empirical analysis showed that this was the case from 2001 to 2009. Conflict was lower when the free riding was greatest. We then took this exact model and tested whether it stood up against data during 2010. Our results show that the network model of free riding in multilateral conflicts was an improvement over models that only had structural aspects such as economic growth, characteristics of the regime, and the existence of conflict in the region.
This research is based on a use of a large amount of textual information as data, an emerging methodology in recent months. It also takes advantage of the network effects in conflict situations, also a newly emerging approach. Further, it uses current advances in strategic thinking (i.e., game theory) to specify what should be expected. We use the case of Thailand to show that free riding in networks does affect conflict dynamics. In fact, the model is sufficient robust that it allows better predictions for new data, than do more standard approaches. Additional projects of our group can be found at mdwardlab.com.

It is published this month in the American Journal of Political Science, volume 57, Nr. 4 (October), pages 892-912. The authors are Nils W. Metternich, Cassy Dorff, Max Gallop, Simon Weschle, and Michael D. Ward. The paper is available via the AJPS Web site, and in an earlier version.
Related articles
- Six dead in shootout in Thai south (skynews.com.au)
- Thailand begins monitoring of Facebook, YouTube and LINE (dailydot.com)
Pingback: The coup in Thailand and progress in forecasting | Predictive Heuristics
Pingback: The right kind of variance | Predictive Heuristics
Pingback: The right kind of variance | MI Regression